在创建任何复杂的游戏时,您可能需要处理向量</ i0>。它们用于物理学,人工智能,三角学和许多其他情况,但什么是矢量?嗯,简单地说,矢量是一个有方向的数字。让我们首先看一个1维向量,它与单个数字相同,是绘制的一个从零开始到5结束的箭头。这是向量 a ,其等于5,并且如果我们绘制从5开始并且在8结束的另一个箭头,则我们具有等于3的向量 b </ i2>。 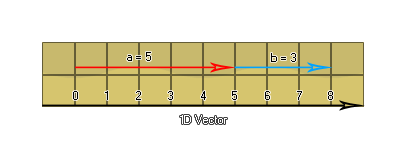
你应该意识到, 一个向量开始并不重要,重要的是它有多长以及它进入的方向。因此,向量 b 从5开始,长度为3个单位并指向“右”,使其与从0开始并且变为3的向量相同。现在,您还可以将这些向量加起来,将两个向量 a 和 b 结束,以获得相等的向量 c 到8。负数呢?好吧,如果在上面的图像中,指向“右”的向量对应于正数,则可以看到指向“左”的向量将对应于负数,从而使得一维向量和 有符号(+/-)数并没有什么不同。这解释了向量的基本概念:只有长度和方向(在这种情况下为“左”或“右”)计数,而不是位置。
那二维向量又怎么样呢?好吧,我们可以认为它们不仅包括“左”和“右”,而且还包括“向上”和“向下”: 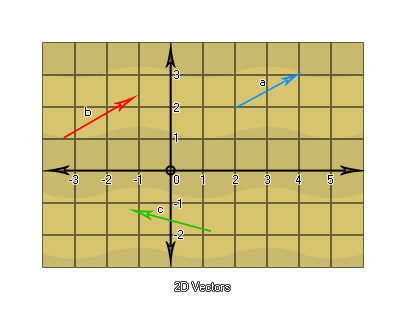
现在,那些实际上并不是矢量,因为我们仍然需要使用它们的起点和终点坐标来减少它们。看看vector a </ i0>我们可以看到它的起始坐标为[2,2],结束坐标为[4,3],所以为了得到这个向量,我们需要将它减少 从起始坐标减去结束坐标,如下所示:[(x2-x1),(y2-y1)] = [(4-2),(3-2)] = [2,1]。现在我们对向量 b做同样的事: [(-1.2 -(-3.2)) ,(2.1 - 1.1)] = [2 ,1]. 注意到什么嘛?这两个向量相同!这是另一个证明向量没有位置,只有方向和长度的示例,我们可以围绕局部[0,0]轴相对于彼此绘制这些向量: 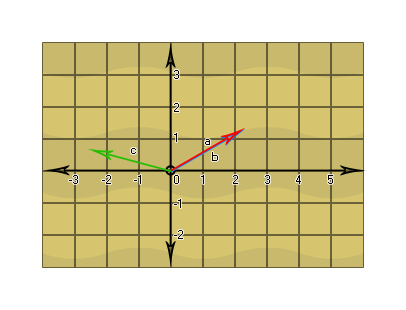
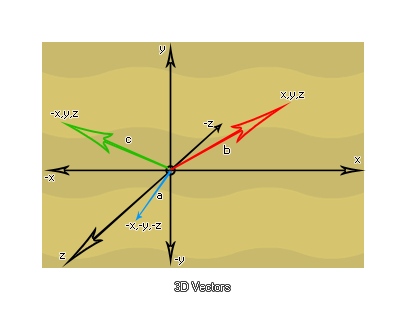
这意味着2D矢量由两个值定义,即相对于局部[0,0]轴的 x </ i0>和 y 位置。3维矢量又如何呢?那么,它们具有“深度”的附加维度,计算将包括 x </ i2>, y </ i3>和 z ,就像这样: